अध्याय 8 – गति – class 9 science chapter 8 notes in hindi

इस पोस्ट में हम Bihar board class 9 science chapter 8 notes in hindi Solutions अध्याय 8 – गति के बारे में चर्चा कर रहे हैं। यदि आपके पास इस अध्याय से संबंधित कोई प्रश्न है तो आप कमेंट बॉक्स में टिप्पणी करें

यह पोस्ट बिहार बोर्ड परीक्षा के दृष्टिकोण से बहुत महत्वपूर्ण है। इसे पढ़ने से आपकी पुस्तक के सभी प्रश्न आसानी से हल हो जायेंगे। इसमें सभी पाठों के अध्यायवार नोट्स उपलब्ध कराये गये हैं। सभी विषयों को आसान भाषा में समझाया गया है।

ये नोट्स पूरी तरह से NCERTऔर SCERT बिहार पाठ्यक्रम पर आधारित हैं। इसमें विज्ञान के प्रत्येक पाठ को समझाया गया है, जो परीक्षा की दृष्टि से बहुत महत्वपूर्ण है। इस पोस्ट को पढ़कर आप बिहार बोर्ड कक्षा 9 विज्ञान के किसी भी पाठ को आसानी से समझ सकते हैं और उस पाठ के प्रश्नों का उत्तर दे सकते हैं।

गति – class 9 science chapter 8 notes in hindi

-:- अध्याय 8 – गति -:-

गति (Motion): जब कोई वस्तु समय के साथ अपनी स्थिति में भी परिवर्तन करती है तो कहा जाता है कि वस्तु की गति में है | जैसे – उड़ते हुए पक्षियों की गति, कार कि गति, धमनियों एवं शिराओं में रक्त की गति, दौड़ते हुए बालक की गति | 

मूल-बिंदु(Origin): किसी वस्तु की स्थिति को बताने के लिए हमें एक निर्देश बिंदु कि आवश्यकता होती है, जिसे मूल बिंदु कहते हैं | जैसे – कोई आम बोल-चाल कि भाषा में कहता है की इस चौराहे से रेलवे स्टेशन 20 किलोमीटर उत्तर में हैं | 

दुरी (Distance): किसी वस्तु द्वारा किसी समय अन्तराल में तय की गए मार्ग कि लम्बाई को उस वस्तु द्वारा चली गयी दुरी कहते है | 

विस्थापन (Displacement): किसी वस्तु के प्रारंभिक स्थिति तथा अंतिम स्थिति के बीच के न्यूनतम दुरी को वस्तु का विस्थापन कहते हैं | 

परिमाण (Magnitiude): किसी भौतिक राशि के संख्यात्मक मान को इसका परिमाण कहते है | 

सदिश एवं अदिश राशि : 

सदिश राशि (Vector Quantity): वह भौतिक राशि जिसके परिमाण (maginitide) एवं दिशा (direction) दोनों होते हैं | उसे सदिश राशि कहते हैं |  उदाहरण: भार, विद्युत आवेश, वेग, बल, संवेग, विस्थापन आदि | 

अदिश राशि (Scalar Quantity): वह भौतिक राशि जिसके केवल परिमाण () होता है दिशा नहीं होता है उसे अदिश राशि कहलाती है | उदाहरण: भार , समय. क्षेत्रफल, आयतन, चाल, दुरी, ताप, घनत्व आदि | 

सरल रेखीय गति : जब कोई वस्तु किसी सरल रेखीय पथ पर गतिमान हो तो उसे सरल रेखीय गति कहते हैं |  

दुरी एवं विस्थापन का उपयोग: 

• (i) दुरी एवं विस्थापन का प्रयोग वस्तु कि पूरी गति प्रक्रिया को व्यक्त करने में किया जाता है |
• (ii) दिए गए समय में वस्तु कि प्रारंभिक स्थिति के सापेक्ष अंतिम स्थिति ज्ञात करने में किया जाता है | 

दुरी (Distance): 

• (i) यह वस्तु द्वारा तय किये गए मार्ग की कुल लम्बाई होती है | 
• (ii) यह एक अदिश राशि है |
• (iii) दुरी सदैव धनात्मक होती है | 
• (iv) यह विस्थापन से बड़ा या बराबर होती है | 
• (v) यह मार्ग कि लम्बाई पर निर्भर करता है | 

विस्थापन (Displacement): 

• (i) यह वस्तु की प्रारंभिक स्थिति तथा अंतिम स्थिति के बीच कि न्यूनतम दुरी होती है | 
• (ii) यह एक सदिश राशि हैं | 
• (iii) विस्थापन धनात्मक, ऋणात्मक एवं शून्य भी हो सकता है | 
• (iv) यह दुरी से छोटा अथवा बराबर होता है | 
• (v) यह मार्ग कि लंबाई पर निर्भर नहीं करता है | 

एकसामान गति : जब कोई वस्तु समान समयांतराल में सामान दुरी तय करती है तो उसकी गति को एकसामान गति कहते हैं | 

असमान गति : जब कोई वस्तु सामान समयांतराल में असमान दुरी तय करती है तो इस प्रकार कि गति को असमान गति कहते हैं | 

चाल (speed) : किसी वस्तु द्वारा इकाई समय में तय कि गयी दुरी को चाल कहते है | 

• चाल का मात्रक मीटर (m) प्रति सेकेंड है | 
• चाल के अन्य मात्रक है, सेंटीमीटर प्रति सेकंड है एवं किलोमीटर प्रति घंटा |  
• चाल एक अदिश राशि है | 
• यह सदा धनात्मक होता है | 
• वस्तु कि गति को व्यक्त करने के लिए हमें केवल उसके परिमाण कि आवश्यकता होती है | दिशा कि कोई आवश्यकता नहीं होती है | 

अधिकतर अवस्थाओं में वस्तुएँ असमान गति करती करती हैं | ऐसी वस्तुओं कि गति कि दर ज्ञात करने के लिए औसत चाल ज्ञात करते हैं | 

वेग (Velocity) : जब कोई राशि किसी वस्तु की चाल में परिमाण के साथ-साथ दिशा को भी व्यक्त करे तो ऐसे चाल को वेग कहते है | 

परिभाषा : एक निश्चित दिशा में वस्तु कि चाल को वेग कहते है | वेग का मात्रक मीटर प्रति सेकंड m s^-1 या m/s होता है | 

• किसी वस्तु का वेग समान एवं असमान हो सकता है | 
• वेग एक सदिश राशि है | 
• इसमें वस्तु की चाल निश्चित दिशा में होता है | 

जब एक वस्तु सीधी रेखा में बदलती हुई चाल के साथ गति कर रही है ती हम इसकी गति कि दर के परिमाण को औसत वेग के रूप में व्यक्त करते हैं | 

वेग के प्रकार: 

(A) एकसमान वेग (uniform velocity): जब कोई वस्तु समान समयांतराल में समान विस्थापित होती है, तो वस्तु के इस प्रकार के वेग को एकसमान वेग कहते है | 

(B) असमान वेग (Non-uniform velocity): जब कोई वस्तु समान समयांतराल में असमान विस्थापित होती है, तो वस्तु के इस प्रकार के वेग को असमान वेग कहते है | 

(C) औसत वेग (Average velocity):  किसी गतिमान वस्तु का औसत वेग उसके प्रारंभिक वेग और उसके अंतिम वेग का अंकगणितीय माध्य होता है | 

चाल (speed): 

• (i) यह इकाई समय में वस्तु वस्तु द्वारा तय दुरी है |
• (ii) यह एक अदिश राशि है |
• (iii) किसी गतिमान वस्तु का औसत चाल शून्य नहीं हो सकता है | 
• (iv) किसी वस्तु कि चाल हमेशा धनात्मक होता है |

वेग (velocity): 

• (i) यह इकाई समय में वस्तु द्वारा तय विस्थापन होता है | 
• (ii) यह एक सदिश राशि है | 
• (iii) किसी गतिमान वस्तु का औसत वेग शून्य हो सकता है | 
• (iv) किसी वस्तु का वेग धनात्मक, ऋणात्मक अथवा शून्य हो सकता है | 

त्वरण (accelaration): इकाई समय में किसी वस्तु के वेग परिवर्तन की दर को त्वरण कहते है | इसको ‘a’ से सूचित किया जाता है | और इसका SI मात्रक ms^-2 होता है | 

एकसमान सरल रेखीय गति में वेग में परिवर्तन :

• समय के साथ वेग नियत रहता है | 
• इस अवस्था में किसी भी समयान्तराल में वस्तु के वेग में परिवर्तन शून्य है | 

असमान गति में वेग में परिवर्तन : 

• असमान गति में वेग समय के साथ परिवर्तित होता है |
• इसका मान विभिन्न समयों पर विभिन्न बिन्दुओ पर भिन्न-भिन्न होता है |
• किसी भी समयान्तराल पर वस्तु के वेग में परिवर्तन शून्य नहीं होता है |  

त्वरित गति : यदि किसी वस्तु का वेग उसके आरंभिक वेग का मान u से t समय में अंतिम वेग v है और त्वरण a है तो इस प्रकार के गति को त्वरित गति कहते हैं | 

सूत्र: 

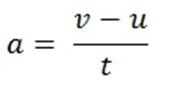
उदाहरण: यदि एक बस विराम अवस्था से शुरू होक 72 km h^-1 की चाल 5 सेकंड में प्राप्त करती है जबकि वह एकसमान गति में है तो बस का त्वरण ज्ञात कीजिए | 

हल: 

समय (t) = 5 मिनट = 5 × 60 = 300 सेकंड

आरंभिक वेग u = 0    [∵ बस विरामावस्था में थी इसलिए आरंभिक वेग शून्य होगा ] 

अंतिम वेग v = 72 km h^-1 

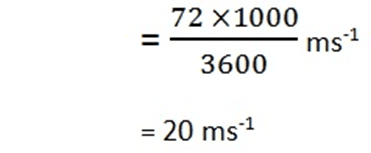
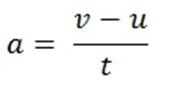
                         = (20 – 0)/300 

                         = 0.066 ms^-2

वस्तु का त्वरण = 0.066 ms^-2

त्वरण के प्रकार : त्वरण के प्रकार त्वरण की दिशा पर आधारित है | ये निम्न प्रकार के हैं :

• (1) धनात्मक त्वरण : 
• (2) ऋणात्मक त्वरण : 

(1) धनात्मक त्वरण : जब किसी वस्तु का वेग वस्तु की गति की दिशा में समय के साथ बढ़ रहा है तो इसे धनात्मक त्वरण कहते है | 

• इसमें त्वरण की दिशा वही होती है जो दिशा वस्तु की गति का होता है | 

मुख्य बिन्दुएँ : 

त्वरण धनात्मक होता है : 

• जब त्वरण की दिशा वही होती है जो दिशा वस्तु की गति का होता है |
• जब वेग उसी दिशा में समय के साथ बढ़ता है |
• जब कोई वस्तु विरामावस्था से चलना प्रारंभ करती है | 
• जब अंतिम वेग आरंभिक वेग से बड़ा हो (v > u) | 

(2) ऋणात्मक त्वरण : यदि किसी वस्तु का वेग समय के साथ वस्तु की गति के विपरीत दिशा में कम हो रहा है तो इस प्रकार के त्वरण को ऋणात्मक त्वरण कहते हैं |  ऋणात्मक त्वरण को मंदन कहते हैं | 

मुख्य बिन्दुएँ : 

त्वरण ऋणात्मक होता है : 

• जब त्वरण की दिशा वस्तु के गति के दिशा की विपरीत दिशा में हो | 
• जब वेग समय के साथ कम हो रहा हो |
• जब वस्तु विरामावस्था की ओर जा रही हो | 
• जब अंतिम वेग आरंभिक वेग से कम हो | 

एकसमान त्वरण : जब किसी वस्तु का वेग समान समयांतराल में समान त्वरण उत्पन्न कर रही है तो वस्तु के ऐसे त्वरण को एकसमान त्वरण कहते हैं | 

एकसमान त्वरित गति : किसी वस्तु की गति से एकसमान त्वरण उत्पन्न हो रहा हो तो इस गति को एकसमान त्वरित गति कहते हैं | 

एकसमान त्वरित गति के उदाहरण:

• (i) चिकनी सतह पर लुढ़कते हुए गेंद की गति |
• (ii) मुक्त रूप से गिरते हुए किसी पिंड की गति |
• (iii) सूर्य के चारो ओर पृथ्वी की गति |
• (iv) एक बहुमंजिली ईमारत से नीचे आती एक तीव्र गति के लिफ्ट की गति |
• (v) पृथ्वी के चारों ओर चन्द्रमा की गति |

असमान त्वरण : जब किसी वस्तु का वेग समान समयांतराल में असमान त्वरण उत्पन्न कर रही है तो वस्तु के ऐसे त्वरण को एकसमान त्वरण कहते हैं |

असमान त्वरित गति: जब किसी वस्तु की गति से भिन्न-भिन्न त्वरण उत्पन्न हो रहा हो तो ऐसे गति को असमान त्वरित गति कहते हैं | 

असमान त्वरित गति के उदाहरण: 

• (i) एक कार रेस में दौड़ती हुई कार | 
• (ii) विभिन्न चाल से चलती हुई वाहन की गति | 
• (iii) ऊपर की दिशा में फेंकी गई गेंद की गति |
• (iv) खुरदरे या टूटे फूटे सड़क से गुजरती हुई बस की गति | 

गति का ग्राफीय प्रदर्शन : ग्राफ का प्रयोग किसी वस्तु की गति को प्रदर्शित करने के लिए किया जाता है | अनेक प्रकार के घटनाओं के विषय में अधारभूतिक सूचनाओं को प्रदर्शित करने के लिए ग्राफ एक सुविधाजनक विधि प्रदान करता है | 

उदाहरण: 

• (i) एक दिवसीय क्रिकेट मैच के प्रसारण में |
• (ii) प्रत्येक ओवर में टीम के रन रेट को दर्शाते उर्ध्वाधर दंड आलेख | 
• (iii) आपने गणित के विषय में पढ़ा है कि एक सरल रेखीय ग्राफ दो चर में रैखिक समीकरणों को हल करने में मदद करता है | 

भौतिकी विज्ञान में ग्राफ का प्रयोग : 

• (i) दो वस्तुओं की गति की तुलना करने लिए ग्राफ बहुत ही उपयोगी होता है | 
• (ii) दुरी-समय ग्राफ से समय के किसी भी बिंदु पर वस्तु की स्थित का पता लगाया जा सकता है | 
• (iii) वेग-समय ग्राफ की ढाल किसी वस्तु की त्वरण को बताता है |
• (iv) सरल रेखीय ग्राफ दो चर में रैखिक समीकरण को हल करने में मदद करता है | 
• (v) दुरी-समय ग्राफ बताता है कि कब और कहाँ कोई वस्तु किसी अन्य वस्तु को पार करती है | 

किसी वस्तु के गति का वर्णन करने के लिए एक भौतिक राशि है जैसा कि दुरी या वेग एक अन्य दूसरी राशि समय है | 

गति को प्रदर्शित करने के लिए दो शर्त है : 

• (i) किसी वस्तु का समय के साथ स्थिति में परिवर्तन को दुरी-समय ग्राफ के द्वारा प्रदर्शित किया जा सकता है | 
• (ii) सरल रेखा में गतिमान किसी वस्तु के लिए समय के साथ वेग में बदलाव को वेग-समय ग्राफ से प्रदर्शित किया जा सकता है | 

1. दुरी-समय ग्राफ : इस ग्राफ में : 

• समय को x-अक्ष के साथ लिया जाता है और दुरी को y-अक्ष के साथ लिया जाता है |
• दुरी-समय ग्राफ को बहुत से शर्तों के अंतर्गत नियोजित किया जा सकता है जहाँ वस्तुएँ एकसमान चाल से, असमान चाल  से गति करती है या विराम अवस्था में रहती है | 

​मुख्य अवधारणायें : वस्तु द्वारा तय दुरी उसके द्वारा लिए गए समय के अनुक्रमानुपाती होता है | 

दुरी-समय ग्राफ में दो प्रकार के ग्राफ होते हैं :

(i) एकसमान चाल के लिए दुरी-समय ग्राफ:

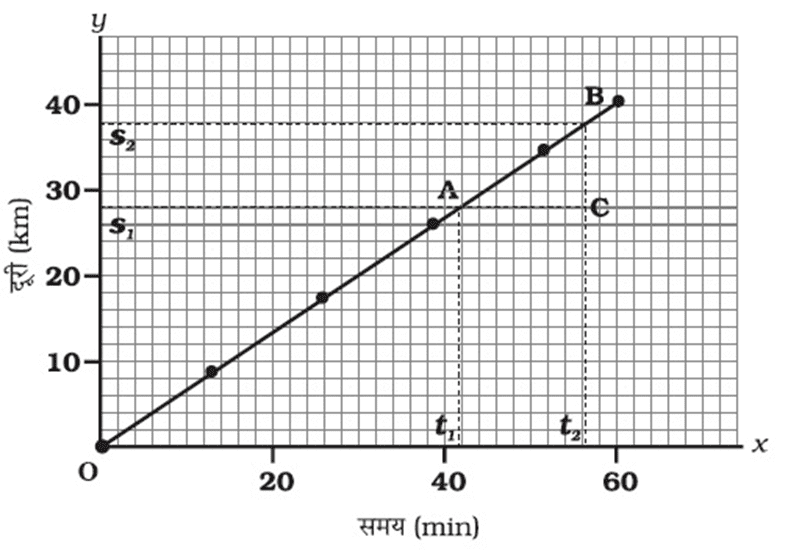
एकसमान चाल के लिए दुरी-समय ग्राफ की प्रकृति :

(a) इसका ग्राफ एक सरल रेखा होता है | 

चाल के लिए सूत्र : 

(ii) असमान चाल के लिए दुरी-समय ग्राफ:

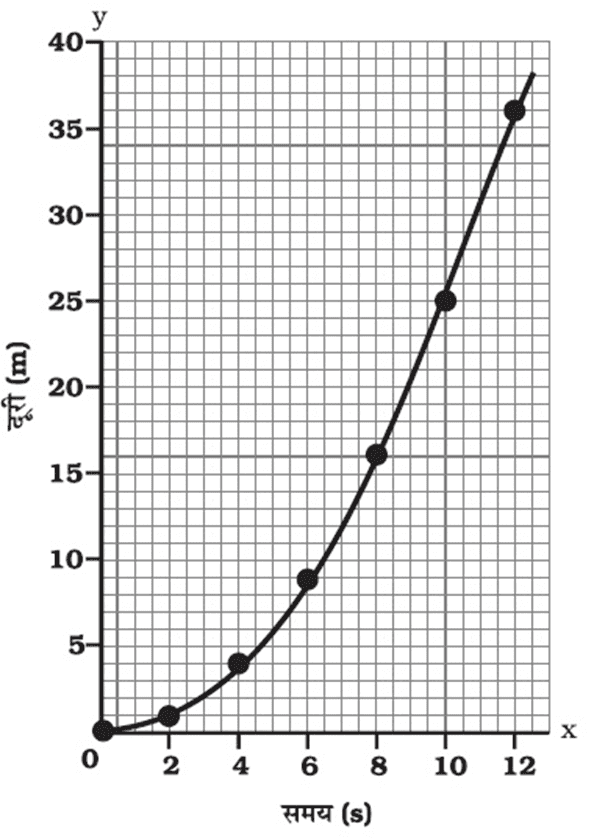
असमान चाल के लिए दुरी-समय ग्राफ की प्रकृति :

(a) इसका ग्राफ एक वक्र रेखा होता है | 

वेग-समय ग्राफ : इस ग्राफ में,

• समय को x अक्ष पर और वेग को y-अक्ष पर  दर्शाया जाता है | 
• यदि वस्तु एकसमान वेग से गतिमान है, तो समय के साथ वेग समय ग्राफ की ऊँचाई में कोई परिवर्तन नहीं होगा | 
• वेग-समय ग्राफ तथा समय अक्ष के द्वारा घेरा गया क्षेत्र विस्थापन के परिणाम को बताता है | 

वेग-समय ग्राफ तीन प्रकार के होते हैं |

(i) एकसमान चाल के लिए वेग-समय ग्राफ 

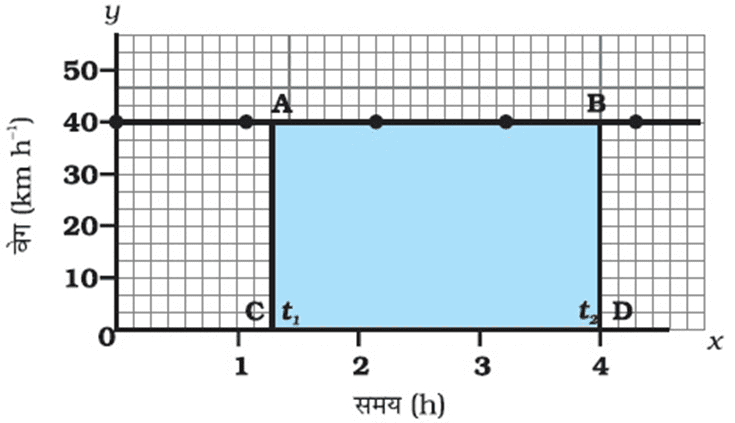
(ii) एक समान त्वरित गति के लिए वेग-समय ग्राफ  

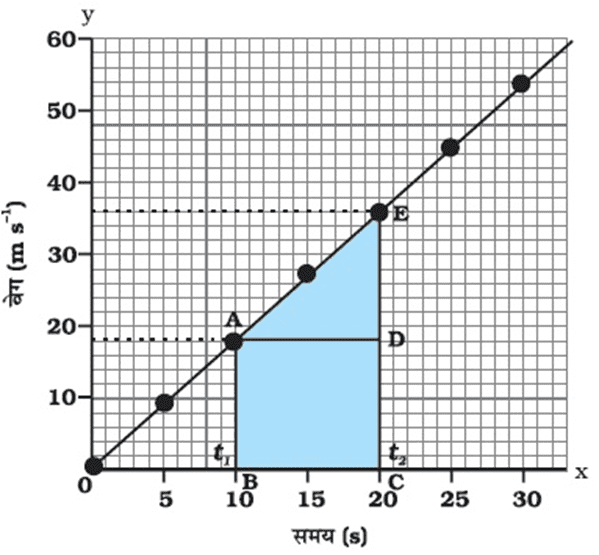
(iii) असमान त्वरित गति  के लिए वेग-समय ग्राफ

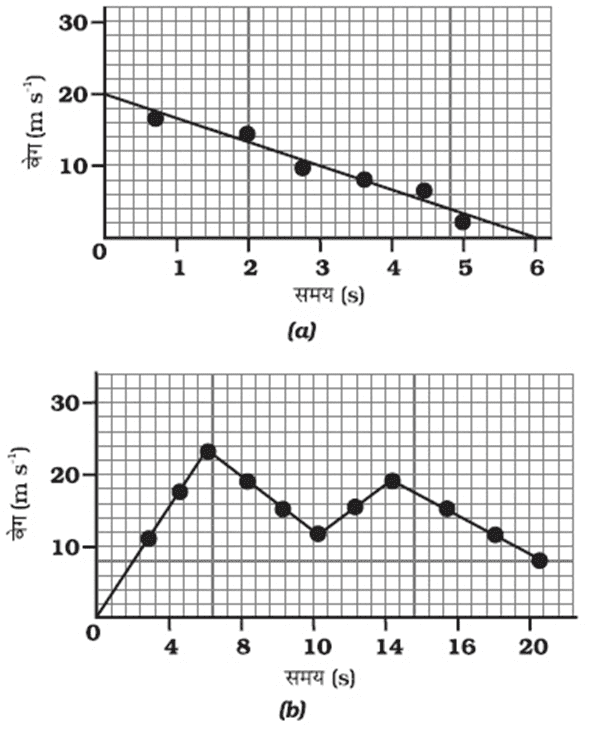
ग्राफीय विधि से गति के लिए सूत्र : कोई वस्तु सीधी रेखा में एकसमान त्वरण से चलती है तो एक निश्चित समयांतराल में समीकरणों के द्वारा उसके वेग, गति के दौरान त्वरण व उसके द्वारा तय की गई दूरी में जो संबंध स्थापित होता है, उस समीकरण को गति का समीकरण कहा जाता है | ये समीकरण तीन हैं –

• (i)   v = u + at      
• (ii)  s = ut +  ½ at²
• (iii) 2 as = v² – u²

गति के समीकरण को प्राप्त करने के लिए वेग-समय ग्राफ – 

•  इस वेग समय ग्राफ में OE रेखा या BC रेखा वेग को प्रदर्शित करता है जबकि OC रेखा समय को प्रदर्शित करता है | 
• BE तिरछी रेखा समयानुसार वेग में परिवर्तन (त्वरण) को प्रदर्शित करता है |
• वेग समय ग्राफ से वस्तु के त्वरण को व्यक्त किया जाता है |  

(i)   v = u + at  के लिए हल : 

अब, BC = BD + DC 

= BD + OA …………. (i) 

यहाँ आरंभिक वेग (u) = OA है और 

अंतिम वेग (v) = BC है | 

इसलिए, BC = v तथा OA = u रखने पर 

     BC = BD + OA   समी० (i) से 

या    v = BD + u 

या  BD = v – u  

अत: वेग में परिवर्तन BD = v – u ………… (ii)

लिया गया कुल समय (t) = OC 

BD = at   ………… (iii) 

समीकरण (ii) तथा (iii) से 

    v – u = at 

या  v = u + at  

(ii)  s = ut +  ½ at² के लिए हल : 

अब, 

माना वस्तु ने एकसमान त्वरण a से t समय लगाकर s दुरी तय की | 

वस्तु द्वारा तय की गई दुरी = वेग-समय ग्राफ में AB के नीचे घिरे क्षेत्र OABC का क्षेत्रफल 

अत : s = समलंब OABC का क्षेत्रफल 

या     = आयात OADC का क्षेत्रफल + त्रिभुज ABD का क्षेत्रफल 

       = OA × OC + ½ (AD × BD) 

       = u × t + ½ × (t × at)  [चूँकि BD = at] समी० (iii) से 

       = ut + ½ at² 

अत: s = ut + ½ at²​  

(iii) 2 as = v² – u² के लिए हल : 

​अब, उसी प्रकार 

वेग समय ग्राफ से – 

    v – u = at 

या  

s = समलंब OABC का क्षेत्रफल 

  = ½ (समांतर भुजाओं का योग‘) × ऊँचाई

  = ½ (OA + BC) × OC

  = ½ (u + v) × t      समी० (1) से 

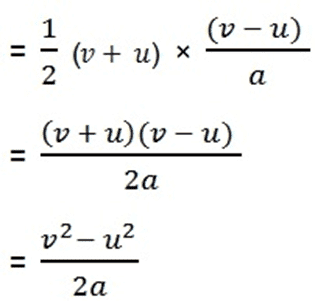
या 2 a s = v² – u²